

Multicolored Logical Net Modeling Formalism
A Discrete Symbolic Dynamical System (DSDS) is a set of system components. The components and the system are perceived via a set of their properties. The properties describe the components and the system characteristics. All properties of DSDS are qualitative. For instance, we may say: "The Earth is orbiting the Sun". Here, "The Earth" and "The Sun" are the components of the system, and "is orbiting the Sun" is the property of the component Earth.
Some component properties can never change, and therefore are considered to be static, while some others may change over time and, therefore, are considered to be dynamical. When property changes over time, we say: "The property takes different states at different times".
The state of a component is defined as a combination of the states of the component properties. The state of the system, as a whole, is the combination of the states of all its components and, hence, is the combination of the states of all the system component properties. The system behavior is observed as a sequence of the states the system properties take over time.
The Multicolored Logical Net (McLN) modeling formalism (MF) is a graphical construction set developed (1) to represent modeled DSDS component properties and their states, and (2) to specify and replicate modeled DSDS behavior by simulating in the model the same sequences of each property state-to-state transitions that we observe in the modeled system.
The task of modeling of DSDS behavior with McLN MF is achieved by defining a set of Property State Dependency Rules that map some combinations of states of some certain subsets of all modeled properties to some particular states offered to some other subsets of the properties to take.
Created with the McLN MF, DSDS McLN model (or briefly the McLN model) is a virtual device depicted on the computer screen. A desktop or web-based McLN development environment can provide a means to create a McLN model, save it, retrieve, edit, and simulate its behavior. Working McLN model examples can be found on the "McLN Viewer". page. The example of a simple McLN model is depicted in Figure 1.

Figure 1. McLN model: "Trigger".
McLN Model Structure
The McLN model structure is a directed bipartite graph. The graph consists of two types of nodes: Properties and Conditions. Directed arcs connect Properties to Conditions and Conditions to Properties.
Property nodes represent modeled DSDS properties and are depicted as circles. Property states are represented as a solid color that fills the circle. As a dynamical property can take different states at different times, a list of property's possible states is created and associated with corresponding Property node at the time of model development.
Condition nodes represent property state dependency rule conditions and are depicted as small circles. They are filled in with either white or gray color. White color represents a Condition's satisfied state, while gray color represents a Condition's not satisfied state.
Arcs represent dependency of the state of the nodes from the state of some other nodes and are depicted as arrows with an arrow head indicating the arc direction and pointing to the dependent node. Arcs directed to a node are considered to be the node's input arcs, while the node is considered to be the arcs' output node. Respectively, arcs directed from a node are considered to be the node's output arcs, while the node is considered to be the arcs' input node.
Each arc directed from Property to Condition is marked with one of its input Property's possible states. Each arc directed from Condition to Property is marked with one of its output Property's possible states. The marking state is represented as a color that fills in the arc arrow head.
Properties connected to a Condition by the Condition's input arcs are considered to be the Condition's input Properties. Respectively, Properties connected to a Condition by the Condition's output arcs are considered to be the Condition's output Properties.
Each modeled Condition, its input and output Properties, as well as all arcs connecting the Properties to the Condition and the Condition to the Properties constitutes the McLN model Property State Dependency Rule, also known as "If-Then" rule. All the Condition's input Properties are considered to be the rule's precondition or premise Properties, while all the Condition's output Properties are considered to be the rule's conclusion Properties. Each Property can be a premise Property and a conclusion Property at the same time.
The state of a model Property is typically controlled by several dependency rules. The example of the McLN model structure where the state of one conclusion Property is controlled by three dependency rules is depicted in Figure 2.
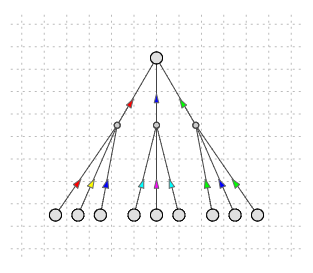
Figure 2. One conclusion Property is controlled by three dependency rules.
Each rule has its own set of three premise Properties.
Modeling DSDS Behavior
When describing McLN model behavior, we consider all parts of the model: Properties, Conditions and arcs to be simple functional devices. Thus, each part has its input and output and is capable of receiving a signal of a state as its input, processing the signal, and emitting a derived signal as its output. A model is assembled by connecting the outputs of parts to the inputs of other parts. For instance, the outputs of the nodes are connected to the inputs of their output arcs, and the outputs of the arcs are connected to the inputs of their output nodes.
The Property nodes' basic function is to take and to hold the property's current state.
The arcs from Properties to a Condition are "State Recognizers". The marking state of an arc-recognizer is one of the arc's input Property's possible states that is considered to be the Property Expected State. The role of these arcs is to check if the arc's input Property's state is equal to the arc's Expected State. When Property takes the state that is equal to the arc's expected state, the signal of the fact that the Property is in the expected state is emitted to the arc's Condition.
The Condition nodes are their input arcs' output collectors. They take signals from their input arcs and evaluate whether the condition is satisfied. The Condition is considered to be satisfied when all its input Properties take the states that are successfully recognized by the Condition's input arcs as the arcs' expected states.
The structure composed of a Condition, all its input state recognizing arcs, and all the arcs' input premise Properties forms a fragment that is a rule condition evaluating expression. The combination of all Properties states is considered to be a situation the rule is supposed to recognize. The output of the fragment is the Condition's state that represents the fact that the expected situation is recognized or not recognized. This fact is depicted on the screen as white or gray color respectively.
The arcs from a Condition to Properties are "State Generators". They identify the group of Properties the states of which are expected to change when the Condition gets satisfied. These arcs generate the state they are marked with. The states generated by the arcs are offered to the arcs' output Properties to take.
The structure composed of a Condition, all its output state generating arcs and all the arc's output Properties form a property state dependency rule that checks the condition and generates the conclusion. This model fragment thus stands for the dependency rule's "If" and "Then" parts.
As each Property may have many state-generating input arcs that are connected to different Conditions and hence can produce different offers of state for the Property to take, the "Rule of Concordance" is applied. It sounds as follows:
(1) If none of the Property's input Conditions is satisfied, the Property state does not change.
(2) If all but one of the Property's input Conditions are not satisfied, the state generated by the Property's input arc connected to the satisfied Condition is taken.
(3) If some of the Property's input Conditions are not satisfied while more than one of the other Conditions appear to be satisfied and their output arcs produce the same offer (same state to take), the offer is considered to be accepted and the Property takes the offered state.
(4) If some of the Property's input Conditions are not satisfied while more than one of the other Conditions appear to be satisfied and their output arcs produce different offers (different states to take), the offers are considered to be competitive and neutralized. So the Property state does not change. The multiple offered states, thus, are exclusive in the McLN.
Examples
This section presents two basic McLN rule structures and explains how associated with Properties, Conditions, and arcs functionality makes the rules work.
Example 1. Figure 3 depicts McLN model's minimal most rule structure. This rule consists of only one premise Property, one recognizing arc, one Condition, one generating arc and one conclusion Property. The condition's input recognizing arc is marked with red color and, hence, is supposed to recognize a situation when its input premise Property is in the red state. The condition's output generating arc is marked with blue color and, hence, is supposed to generate on its output blue state offered for the conclusion Property to take when the condition is satisfied.
Figure 3a represents a situation when the premise Property is in an initial (gray) state. This state is not what is expected by the recognizing arc. So the Condition is not satisfied and its output generating arc does not generate any state offered for the conclusion Property to take. Hence, the conclusion Property is still in its gray state.
Figure 3b represents a situation when the premise Property state changed. It is now in the red state. This state is expected by the recognizing arc. So, the state is recognized and the Condition appears to be satisfied. As a result, the Condition's generating arc is activated and generates on its output blue state offered for the conclusion Property to take. Finally, as the conclusion Property does not have any other input arcs and, hence, there are no other competitive offers, the conclusion Property takes the only offered state and goes blue.
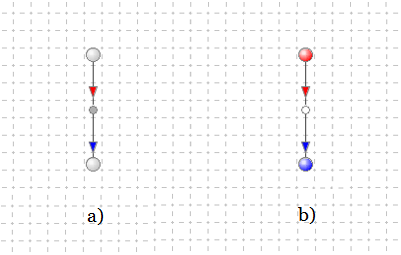
Figure 3. Minimal most dependency rule and McLN model states:
a) state before premise Property changed to red state,
b) state after premise Property changed to red state.
Example 2. Figure 4 depicts McLN model's two rule structure. This structure consists of one conclusion Property the state of which is controlled by two competitive dependency rules. Each rule has its own set of two premise Properties. Figures 4a, 4b, and 4c represent three snapshots made at different times.
Figure 4a depicts the case when the set of two premise properties of the left rule represents a situation that is recognized, while the situation represented by the set of two premise properties of the right rule is not recognized. Thus, only the left rule appears to be satisfied and generates its red state that is offered for the conclusion Property to take. As there is no competitive state offered by the right rule the conclusion Property has taken the red state.
Figure 4b represents the case when the left rule is still recognizing its expected situation and generates its red state that is offered for the conclusion Property to take. However, the right rule is also recognizing its expected situation and generates its blue state that is offered for the conclusion Property to take. As these two competitive rules are offering two different states for the conclusion Property to take, the offered states are considered as competitive and the conclusion Property does not change its current state. In other words it continues to stay in the red state.
Figure 4c depicts the case when the set of two premise properties of the left rule represents a situation that is not recognized, while the situation represented by the set of two premise properties of the right rule is recognized. This time only the right rule is satisfied and generates its blue state that is offered for the conclusion Property to take. As at the moment there is no alternative offer from the left rule, the conclusion Property takes the only offered blue state.
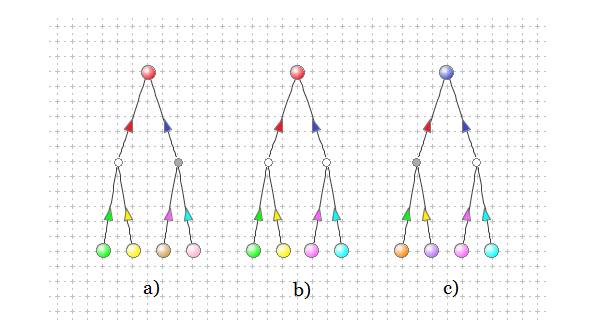
Figure 4. State of conclusion Property is controlled by two dependency rules:
a) only the left rule is satisfied, b) both rules are satisfied,
c) only the right rule is satisfied.
![]()







